انتگرال معین - کاربردهای انتگرال معین

کاربرد انتگرال معین | بلاگ آموزشی لینوم

مساحت رویه های محدود به خم ها، حجم اجسام سه بعدی، طول خم ها، مساحت رویه های خمیده، گشتاورهای لختی، جذر میانگین مربع ولتاژ، نیروهای وارد بر سدها نمونه هایی هستند که همگی را می توان به طور طبیعی به عنوان حد مجموعه های متناهی تعریف کرد. گاه چنانکه در مثال بعد خواهیم دید برای یافتن یک مساحت آسان تر است که به عوضانتگرال گیری از مساحت نوارهای قائم روی بازه ای واقع بر محور ، از نوارهای افقی روی بازه ای واقع بر محور  انتگرال بگیریم. اکنون که می توانیم مساحت بسیاری از نواحی مسطح را حساب کنیم، می توانیم روش تشکیل مجموعهای ریمان را تعمیم دهیم و حجم اجسامی را که این نواحی سطح مقطع های آن ها هستند به دست آوریم.

اما چگونه می توان  را تعریف کنیم، میل داریم که این جسم حداقل برابر  باشد، یعنی برابر با حجم استوانه ای که قاعده آن سطح مقطعی از برش با کمترین مساحت است. اگر این ناحیه، ناحیه ای بین نمودار  ، و محورx  باشد و محور دوران همان محور  باشد، مقطع هایی از جسم که بر محور عمودند و به صورت قرص اند همانند شکل زیر. این تعریف تعمیمی است از فرمول زیر(در هندسه قضایی) در مورد استوانه های مستدیر به استوانه هایی با قاعده های دلخواه، نظیر استوانه ای که در شکل زیردیده می شود. اگر جسمی روی خطی حرکت کند و سرعتش، ، تابعی پیوسته از زمان باشد،به کمک انتگرال گیری می توان تابع مکان جسم را که شامل یک ثابت نامشحص  است به دست آورد.

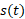
اگر مساحت سطح مقطع جسم در حالت عمود بر محور  تابعی پیوسته چون  باشد، مقدار آن در بازه در نقطه ای چون  مینیمم و در نقطه ای چون  ماکسیمم است. مثلا اگر جسمی از مکان اولیه اش 5 متر به طرف جلو و سپس 5 متر به طرف عقب حرکت کند، تغییر خالص مکانش صفر است در حالی که مسافتی را که می پیماید 10 متر است. برای محاسبه کل مسافت پیموده شده به کمک انتگرال باید به گونه ای عمل کنیم که مسافات پیموده شده در حرکت به جلو و عقب همدیگر را خنثی نکنند. در این نماد، دیفرانسیل  نقش دو گانه ای ایفا می کند، یعنی هم پهنای نوار مستطیلی و هم متغیر انتگرال گیری در انتگرال را نشان می دهد.

 

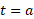
این دو نتگرال تنها در بازه انتگرال گیری با هم تفاوت دارند ، یعنی ما در هر دو حالت عمل انتگرال را ابتدا محاسبه می کنیم ،اما در انتگرال معین پس از بدست آمدن جاصل باید آن را در بازه مشخص اعمال کنیم شکل زیر فرق دو انتگرال را به سادگی نمایش می دهد. پس آنچه در این پست فرا گرفتیم مفهوم اولیه انتگرال است ،و ارتباط انتگرال با عمل مشتق گیری  همچنین کاربردهای آتی انتگرال در محاسبه حجم و مساحتها می باشد ، به عنوان آخرین مطلب این پست مفهوم انتگرال معین و نامعین را هم بطور مختصر بیان می کنیم. به شکل بالا خوب دقت کنید هر کدام از عبارتهای سمت راست را اگر از آنها مشتق بگیریم حاصل همه آنها بعد از مشتق همان عبارت 2x  خواهد بود به همین خاطر ما وقتی از 2x  انتگرال گرفتیم حاصل جواب به اضافه عدد ثابت C  می باشد.

مثلا در شکل بالا ما با داشتن معادله تابع (f(x  و انتگرال گیری از ان تابع می توانیم مساحت محدود زیر این منحنی و محور x  ها را بدست آوریم ، البته روش کار و قانون آن مفصل است که ما در بخشهای دیگر به آن می پردازیم. به تعبیری دیگر در انتگرال نامعین بازه انتگرال گیری مشخص نیست  و فقط هدف ما عمل انتگرال است ،اما در انتگرال معین ما از همان ابتدا بازه انتگرال گیری مشخصی داریم و عمل انتگرال تابع در آن بازه محاسبه می شود. چرا این عدد C  را باید بنویسیم دلیل آن خیلی ساده است ، ببینید اگر چه ما می دانیم که حاصل انتگرال فوق X به توان 2 است اما اصل تابع 2x  ممکن است یکی از حالتهای زیر باشد.

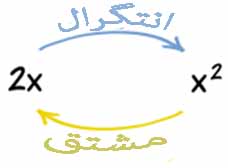
مثلا در بالا نگاه کنید که چگونه مشتق و انتگرال معکوس هم هستند البته فعلا نگران نباشد چون گام به گام روشهای انتگرال گیری را با هم فرا می گیریم. تعریف اول :انتگرال گیری یعنی یافتن مساحت محدود به منحنی ها ،حجم اجسام مختلف ،طول منحنی ها ،مرکز جرم اجسام و کاربردهای دیگر است. اما اگر خود عبارت 2x  را داشته باشیم چگونه می توان به تابعی رسید که اگر از آن مشتق بگیریم حاصل عبارت ما برابر با 2x  می شود. انتگرال گیری دو معنی و مفهوم در حساب دیفرانسیل و انتگرال دارد ، هر دو تعریف از دیدگاه ریاضی صحیح و پذیرفته شده است. در واقع ما با انتگرال گیری از تابع می توانیم اصل تابع را قبل از عمل مشتق گیری را بدست آوریم.

 

کاربردهای انتگرال در زندگی روزمره و علوم گوناگون

ریاضیات نقش مهمی در زندگی ما انسان ها ایفا می کند و حساب دیفرانسیل و انتگرال یا حسابان به عنوان یکی از زیر شاخه های پر کاربرد و شناخته شده در این رشته است که دانشمندان و محققان آن را به عنوان ابزاری مفید در تاریخ تمدن می دانند در حالی که بسیاری از دانش آموزان و دانشجویان به آن به چشم مفاهیم دشواری نگاه می کنند که در زندگی واقعی کاربردی ندارند. بدون شک شکل استخر را تعیین کرده و مساحت آن را پیدا می کنیم، اگر شکل استخر یک مکعب مستطیل و یا سایر شکل های منظم باشد محاسبه مساحت آن کار سختی نیست و هر دانش آموزی می تواند آن را حساب کند اما اگر شکل استخر یک شکل هندسی معمولی نباشد با چه کار کرد؟.

یک خودرو از کارخانه خارج نمی شود مگر آن که مواردی همچون مرکز جرم و محور مرکزی خودرو مشخص باشد زیرا این عوامل در حفظ امنیت و ایمنی خودرو در جاده ها و سرعت های مختلف بسیار اهمیت دارد و این موارد تنها با کمک انتگرال و حسابان قابل محاسبه می باشد. مطالعه شیوع بیماری های عفونی مسری به حسابان و مفهوم انتگرال وابسته است، از انتگرال می توان برای تعیین گستره و سرعت شیوع بیماری، این که بیماری از کجا آغاز شده و چگونه به بهترین شکل ممکن می توان آن را درمان کرد استفاده کرد. انتگرال از شاخه های مهم ریاضیات است که مطالعه رسمی آن در قرن 17 میلادی توسط دانشمندان و ریاضی دانان معروفی همچون اسحاق نیوتن و گوتفرید لایبنیتس آغاز شده است، اگرچه تاریخچه استفاده از آن به یونان باستان باز می گردد.

انتگرال در فیزیک کاربردهای زیادی دارد، به عنوان مثال برای محاسبه مرکز جرم، مرکز گرانشی و گشتاور اینرسی جرم یک وسیله نقلیه، ماهواره ها، برج و اساسا هر ساختمان یا سازه دیگری که بتوان تصور کرد به انتگرال نیاز داریم. این زیر شاخه از توابع، حد، مشتق، انتگرال و غیره صحبت می کند و دو مفهوم مهم ریاضی را در خود گنجانده است که شامل حساب دیفرانسیل – مشتقات تابع، رفتار و میزان تغییرات مقادیر مختلف – و انتگرال می باشد. اگر استخر با یک شیب جزئی شروع شود و پس از آن شیب تند شود، سپس طرفین استخر خمیده یا نیمه بیضوی شوند و سپس کمی بالا برود چه؟ آیا یافتن حجم آب مورد نیاز برای پر کردن این استخر آسان است؟.

 

منبع